로지스틱 회귀의 경사 계산 벡터화 | Vectorizing Logistic Regression's Gradient Computation

@벡터화를 통해 m개의 전체 훈련 샘플에 대한 경사 계산(Gradient Computation) 하는 법

 

경사 계산을 위해 첫번째 샘플의 dz^(1)인 a^(1) - y^(1) 계산

dz^(2), …

 

 

dZ 정의

dz^(1), dz^(2) 부터 dz^(m)까지 모든 dz를 가로로 쌓은 것(stack horizontally)

(1,m) 행렬 혹은 m차원 열 벡터가 됨

 

 

A와 Y역시 가로로 쌓여있음

 

 

이 정의를 따른다면 dZ가 A - Y로 계산될 수 있다는 걸 알 수 있음

->첫번째 요소는 a^(1) - y^(1), 두번째 요소는 a^(2) - y^(2) 이렇게 계속되기 때문

 

따라서 한 줄의 코드로 이 모든 것을 동시에 계산 가능

 

 

 

누르면 해당 포스트로 이동

위 식 까지가 지난 번에 했던 것(for문 하나 없애기)

 

 

 

@db에 대한 벡터화 구현

모든 dz를 더하고 m으로 나눠주는 것

 

db는 i가 1부터 m까지일 때 dz(i)의 합을 m으로 나눈 값

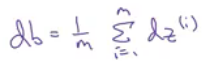
여기서 모든 dz는 열 벡터

 

파이썬에서는 1/m에 np.sum(dZ) 라고 씀

 

단순히 dZ를 가지고 이 함수를 호출하면 db를 반환

 

 

 

@dw

dw는 1/m에 X*dZ^T를 곱한 값

 

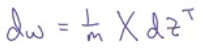
이 값은 1/m에 x^(1)부터 x^(m)이 가로로 쌓인 행렬 X를 곱하고

dZ^T는 dz^(1)부터 dz^(m)까지의 벡터가 됨

 

이 행렬과 벡터를 곱하면

1/m에 x^(1) dz^(1)부터 x^(m) dz^(m)을 모두 더한 값을 곱한 게 됨

 

이 벡터는 (m,1) 벡터이고, dw 값이 됨

 

 

 

벡터화된 도함수의 계산은 아래 식으로 for문 없이 변수의 갱신값을 계산할 수 있게 됨

 

 

 

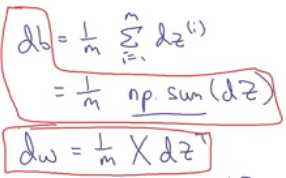
@로지스틱 회귀 구현

-벡터화되지 않은 비효율적인 구현

 

 

-벡터화된 구현(without using for loop)

 

 

경사하강법 갱신은 w = w - αdw

b는 b = b - (학습률α)db 로 갱신됨

 

 

 

경사하강법을 반복하고 싶다면 반복 횟수에 따라 for문이 필요함

 

 

 

 

참고)

https://youtu.be/2BkqApHKwn0