@Vector representation of python
-Vector를 python으로 표현하는 다양한 방법 존재
# There are various ways to represent vectors in Python
vector_a = [1, 2, 10]
vector_b = (1, 2, 10)
vector_c = {'x':1, 'y':1, 'x':10}
print(vector_a, vector_b, vector_c)
# [1, 2, 10] (1, 2, 10) {'x': 10, 'y': 1}-최선의 방법은 없음
-값의 변경 유무, 속성값 유무에 따라 선택 가능
# Vector calculation
u = [2,2]
v = [2,3]
z = [3,5]
result = [sum(i) for i in zip(u,v,z)]
print(result)
# [7, 10]
# Scalar-Vector product
u = [1,2,3]
v = [4,5,6]
alpha = 2
result = [alpha*sum(i) for i in zip(u,v)]
print(result)
# [10, 14, 18]
@Matrix representation of python
-Matrix 역시 python으로 표현하는 다양한 방법 존재
# Matrix representation
matrix_a = [[3,6], [4,5]]
matrix_b = [(3,6), (4,5)]
matrix_c = {(0,0): 3, (0,1): 6, (1,0): 4, (1,1): 5}
print(matrix_a, matrix_b, matrix_c)
# [[3, 6], [4, 5]] [(3, 6), (4, 5)] {(0, 0): 3, (0, 1): 6, (1, 0): 4, (1, 1): 5}-특히 dict로 표현할 때는 무궁무진한 방법이 있음
-위 예시 [[1번째 row], [2번째 row], [3번째 row]]
@Matrix Calculation: Addition
# Matrix addition
matrix_a = [[3,6], [4,5]]
matrix_b = [[3,6], [4,5]]
result = [[sum(row) for row in zip(*i)] for i in zip(matrix_a, matrix_b)]
print(result)
# [[6, 12], [8, 10]]
@Matrix Calculation: Scalar-Matrix Product
# Scalar-Matrix Product
matrix_a = [[3,6], [4,5]]
alpha = 3
result =[[alpha*element for element in i] for i in matrix_a]
print(result)
# [[9, 18], [12, 15]]
@Matrix Calculation: Matrix Transpose(전치)
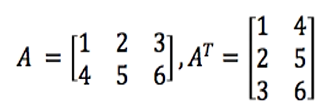
# Matrix Transpose
matrix_a = [[1,2,3], [4,5,6]]
result =[[element for element in i] for i in zip(*matrix_a)]
print(result)
# [[1, 4], [2, 5], [3, 6]]
@Matrix Calculation: Matrix Product

# Matix Product
matrix_a = [[1,1,2], [2,1,1]]
matrix_b = [[1,1], [2,1], [1,3]]
result = [[sum(i*j for i, j in zip(row_a, column_b))
for column_b in zip(*matrix_b)] for row_a in matrix_a]
print(result)
# [[5, 8], [5, 6]]
'CS > Python' 카테고리의 다른 글
| Basic Linear Algebra | 선형대수 기본 (0) | 2021.01.18 |
|---|---|
| News Categorization (0) | 2021.01.18 |
| Data Structure - Collections (0) | 2021.01.13 |
| Asterisk (0) | 2021.01.11 |
| Lambda & MapReduce (0) | 2021.01.11 |




