@Binary Label Encoding -> "0" or "1"
고양이 or not 고양이 같은 범주형(비정형) 데이터들은 반드시 인코딩 되어야 함(0 or 1)
정답 Y는 0과 1로만 구분할 수 있다고 가정
정답을 구하는 데 있어서 모델이 적합하지 않을 수 있음
1보다 크거나 0보다 작거나,,,,
-> 가설 재설정
H(x) = Wx + b
H 값을 0에서 1 사이로 제한 거는 방법?
-> 시그모이드 함수(0과 1 사이로 모든 값을 바운드 시킬 수 있음)
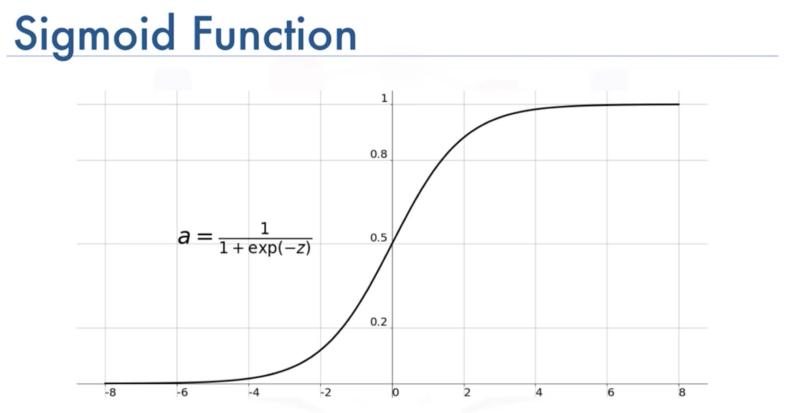
Z = WX 에서
Z 값을 0 < Z < 1
0 에서 1 사이로 바운드 시키기

sigmod 함수 덕분에 H(x)가 바운드됨
Cost function에 적용
기존 선형회귀 cost function에 적용하면 local minima(지역 극소점)에 빠짐
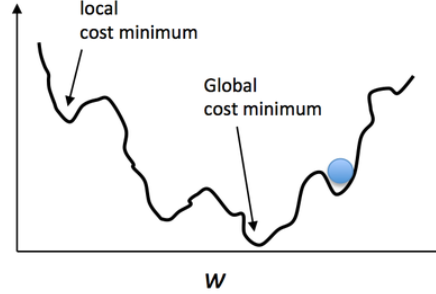
미분 값이 0인 지역이 중간중간 나옴
-> 가설 설정 변경 되었으므로 cost 함수도 재설계!
* cost function : 예측 값(가설 값)이 얼마나 정답에 가까운지 측정하는 척도
설계 팁
- 정답에 가까워질수록 cost function 값 작게
멀어질수록 cost funtion 값 크게!
조건부로 수식이 나눠져 있으면 코딩 시 불편함
하나의 방정식으로 표현하는 게 중요
C(H(x), y) = -ylog(H(x)) - (1-y)log(1-H(x))
요약)
선형 회귀는 이진 분류하는데 문제가 있어서 로지스틱 회귀로 변경,
로지스틱 회귀를 이용하기 위해

시그모이드 함수 이용해 변경했을 때

cost function은 위와 같은 식으로 변경해야 함(재설계)

경사하강법 이용해 W 구할 수 있음
=> 구해진 W로 이진 분류 가능!
'CS > AI | CV' 카테고리의 다른 글
| 이미지 합성 인공지능 #2 (0) | 2021.09.13 |
|---|---|
| 이미지 합성 인공지능 #1 (0) | 2021.09.13 |
| 머신러닝 프로젝트 계획 (0) | 2021.08.31 |
| 선형 회귀 2, Colab 실습 (0) | 2021.07.28 |
| ID Photo Generator | 증명사진 생성기 (0) | 2021.07.26 |




