w, b에 대한 비용 함수(Cost Function)는 평균값
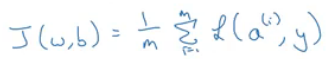
1/m i=1부터 m까지 샘플 y에 대한 출력값 a^(i)의 손실의 합을 곱한 것
비용 함수는 각 손실의 평균이라 할 수 있음

a^(i)는 i번째 샘플의 예측값을 나타내고 sigma(z^(i))와 같음
이는 다시 sigma(w^T*x^(i)+b)와 같음

w_1에 대한 전체 비용 함수의 도함수도 w_1에 대한 각 손실 항 도함수의 평균
단일 훈련 샘플의 도함수를 구해 그 평균을 구하면 경사하강법에 사용할 전체적인 경사 구할 수 있음
@경사하강법을 사용한 로지스틱 회귀 구현 방법
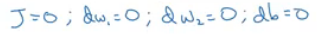
초기화 해줌

각 훈련 샘플에 대한 도함수 계산하고 이를 더함

특성이 두 개(n=2)라고 가정한 것

평균을 계산하는 것이기 때문에 m으로 나눠야 함

dw_1, dw_2, db는 값을 저장하는 데 쓰이고 있음
따라서 계산을 다 하고 나면 dw_1은 w에 대한 전체 비용 함수의 도함수와 같음
dw_2와 db도 마찬가지
dw_1, dw_2는 첨자가 없는데, 훈련 세트 전체를 합한 값을 저장하고 있기 때문
dz^(i)는 훈련 샘플 하나의 dz이기 때문에 계산하고 있는 훈련 샘플 하나를 나타내기 위해 첨자 사용
@경사 하강법 한 단계 구현

경사 하강법을 여러 번 진행하려면 이것을 계속 반복해야 함

@위와 같은 방법으로 로지스틱 회귀를 구현하는 것의 단점
1. 두 개의 for문 필요
첫 번째 for문은 m개의 훈련 샘플 반복
두 번째 for문은 특성 반복
딥러닝 알고리즘을 구현할 때 코드에서 이런 명시적 for문은 알고리즘을 비효율적으로 만듬
딥러닝의 전성기에 들어서면서 데이터 집합이 점점 더 커졌기 때문에 코드를 명시적 for문 없이 구현하는 것이 중요해짐
->그렇게 해야 더 큰 데이터 집합도 처리할 수 있음
->'벡터화'
명시적 for문 제거할 수 있게 해줌
참고)
'CS > AI | CV' 카테고리의 다른 글
| 벡터화 예제 | Vectorization Examples (0) | 2021.01.03 |
|---|---|
| 벡터화 | Vectorization (0) | 2021.01.03 |
| 로지스틱 회귀 경사하강법 | Logistic Regression Gradient Descent (0) | 2021.01.01 |
| 계산 그래프 | Computation Graph (0) | 2020.12.31 |
| 경사하강법 | Gradient Descent (0) | 2020.12.31 |




