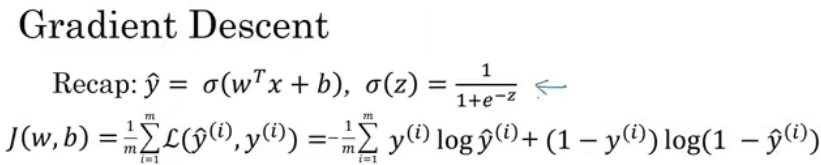
매개변수 w와 b에 대한 함수는 평균으로 정의할 수 있으므로 1/m에 손실 함수의 합 곱함
손실 함수는 각 훈련 샘플의 y의 예측값이 얼마나 좋은지를 각 훈련 샘플에 대한 참값 y hat^(i)와 비교해 측정
비용 함수는 매개변수 w와 b가 훈련 세트를 잘 예측하는지 측정
매개변수 w와 b를 알아내기 위해서는 비용 함수 J(w, b)를 가장 작게 만드는 w와 b를 찾아야 함

위 그래프에서 두 가로축은 매개변수 w와 b의 공간 나타냄
(w와 b가 각각 하나의 실수라고 가정)
비용함수 J(w, b)는 가로축 w, b 위의 곡면이고, 곡면의 높이는 그 점의 J(w, b)값 나타냄
위 특정 비용 함수 J는 활처럼 볼록한(convex) 함수

볼록하지 않은 함수는 지역 최적값이 여러 개
비용 함수는 볼록한 형태여야 함
-볼록하지 않은 함수 쓰게 되면, 경사하강법을 통해 최적의 파라미터 찾을 수 없음
로지스틱 회귀에는 거의 모든 초기화 방법 사용할 수 있지만,
보통 초기값 0으로 설정함
무작위 초기화도 가능하지만 로지스틱 회귀에는 거의 사용하지 않음
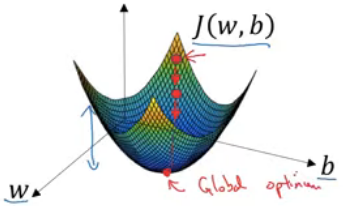
위 함수는 볼록하기 때문에 어디서 초기화를 해도 거의 같은 점에 도착할 것
경사하강법에서는 위 초기점에서 시작해 가장 가파른(steepest) 방향으로 한 단계 내려감
(함수의 기울기를 따라 최적의 값으로 한 스텝씩 업데이트)

@α
-학습률
-경사 하강법 반복할 때 한 단계의 크기를 결정
@dJ(w)/dw
-미분계수
-갱신 시 매개변수 w에 줄 변화를 나타냄
-경사하강법 구현하는 코드 만들 때 관습적으로 미분계수 변수 이름을 dw라 함

-미분계수는 함수의 기울기라고 할 수 있음
-기울기는 J(w)에 접선하는 삼각형의 세로/가로
-위 점의 미분계수는 양수
-w는 w - 학습률 x 미분계수로 갱신됨
-위에서는 미분계수가 양수이므로 w에서 미분계수를 빼는 것이 돼서 왼쪽으로 한 단계 감
->경사하강법은 큰 w에서 시작한 경우, 서서히 매개변수를 감소시킴
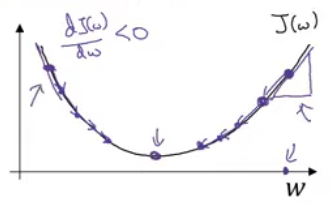
-만약 dw >0 이면, 파라미터 w 는 기존의 w 값 보다 작은 방향으로 갱신,
dw <0 이면, 파라미터 w 는 기본의 w 값 보다 큰 방향으로 갱신

참고)
'CS > AI | CV' 카테고리의 다른 글
| 로지스틱 회귀 경사하강법 | Logistic Regression Gradient Descent (0) | 2021.01.01 |
|---|---|
| 계산 그래프 | Computation Graph (0) | 2020.12.31 |
| 로지스틱 회귀 비용함수 | Logistic Regression Cost Function (0) | 2020.12.31 |
| 로지스틱 회귀 | Logistic Regression (0) | 2020.12.31 |
| 이진 분류 | Binary Classification (0) | 2020.12.31 |




