신경망에서 학습하는 방법은 정방향 전파와 역전파가 있음
@로지스틱 회귀
-이진 분류를 위한 알고리즘

@이진 분류
-그렇다/ 아니다 2개로 분류하는 것
결과가 '그렇다'이면 1, '아니다'이면 0

주어진 사진에 대한 특성 벡터 x를 다음과 같이 정의
R, G, B 픽셀 강도 값 전부를 특성 벡터로 각각 나열
만약 사진이 64 x 64 일 경우 벡터 x의 전체 차원은 64 x 64 x 3이 됨
행렬들의 원소들을 포함하고 있기 때문
위의 경우, 12,288
12,288인 입력 특성 벡터 x의 차원을 n_x로 표현(간결함을 위해 그냥 소문자 n을 쓰기도)
@이진 분류의 목표
-입력된 사진을 나타내는 특성 벡터 x를 가지고 그에 대한 레이블 y가 1인지, 0인지 예측할 수 있는 분류기를 학습

단 하나의 훈련 샘플을 한 쌍(x, y)으로 표시할 때
x는 n_x 차원 상의 특성 벡터이고 레이블 y는 0 또는 1
훈련 세트는 m개의 훈련 샘플을 포함하고 위와 같이 표기
첫 번째 훈련 샘플의 입력과 출력인 (x^(1), y^(1))부터 마지막 훈련 샘플인 (x^(m), y^(m))까지 다 합한 것이 훈련 세트가 됨
위에서는 훈련 샘플의 개수를 m으로 표시함
테스트 세트에 대해서는 테스트 세트의 개수를 m_test로 표시

모든 훈련 샘플들을 더 간결히 표기하기 위해 행렬 x 정의
x의 열들은 입력된 훈련 세트 x^(1), x^(2) 등등으로 이루어져 있음
m이 훈련 샘플의 개수일때 X는 m개의 열과 n_x개의 행들로 이루어져 있음
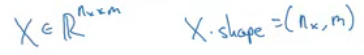
X는 n_x x m 행렬
파이썬을 예로 든다면 X.shape를 해보면 행렬의 차원을 알 수 있음
위 경우에는 (n_x, m)을 출력하게 되고, n_x x m 행렬인 것을 뜻함
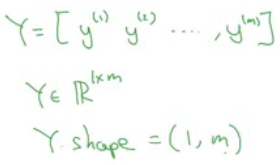
신경망의 구현을 y의 값들을 열로 놓는 것이 편리함
Y는 y^(1), y^(2)부터 y^(m)으로 이루어진 1 x m 행렬로 정의
Y의 차원이 (1, m)임을 알 수 있음
신경망을 만들 때 여기서 X와 Y를 정의한 것처럼 여러 훈련 샘플에 대한 데이터를 각각의 열로 놓는 것이 유용할 것
참고)
'CS > AI | CV' 카테고리의 다른 글
| 계산 그래프 | Computation Graph (0) | 2020.12.31 |
|---|---|
| 경사하강법 | Gradient Descent (0) | 2020.12.31 |
| 로지스틱 회귀 비용함수 | Logistic Regression Cost Function (0) | 2020.12.31 |
| 로지스틱 회귀 | Logistic Regression (0) | 2020.12.31 |
| 신경망(Neural Network), 지도학습(Supervised Learning) (0) | 2020.12.28 |




