모델링
- 현실 세계에서 일어나는 현상을 수학식으로 표현하는 행위
- 모델링을 통해 모델 알아내고 나면 모델 이용해 새로운 사실 예측 가능
데이터 과학에서 주어지는 데이터
- 데이터로부터 모델 알아내야 함
- 주어진 데이터를 훈련 집합이라 함

(xi ,yi )를 i번째 관측observation 또는 i번째 샘플sample이라 부름
독립 변수 xi 를 설명 변수explanatory variable, 종속 변수 yi 를 반응 변수response variable라 부름
또는 xi 를 특징feature, yi 를 레이블lable이라 부름
또는 yi 를 그라운드 트루스ground truth라 부름
데이터 과학에서의 모델링 : 훈련 집합 이용해 최적의 모델 찾아내는 과정
데이터 과학이 다루는 문제는 불확실성 개입
- 예) 같은 시간에 같은 사람의 체온 측정하면 시간에 따라 변하기 일쑤
선형 회귀에서는 최적화 문제 풀어야 함
- 최적화는 미분 사용해 해결
- R 제공 함수 : lm

가설 검정
- 확률변수 : 평균(u), 분산(s2), 데이터 크기(n)
- 귀무가설 (H_0) : 모집단 확률변수와 추정치가 차이가 없다는 가설
- 대립가설 (H_1) : 모집단 확률변수와 추정치가 차이가 있다는 가설
- P-값: 귀무 가설이 맞다는 가정하에서 실험 데이터가 나올 확률을 의미
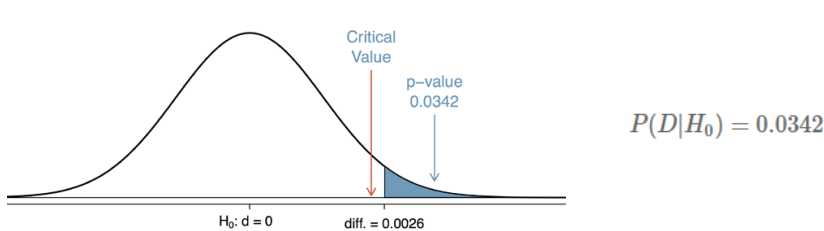
- P-값이 유의 수준 𝜶보다 작으면 통계적으로 유의미함
- 유의 수준 𝜶는 보통 0.05 또는 0.01
R의 cars 데이터 사용해 모델링, 예측
- str(), head()로 데이터 내용 확인
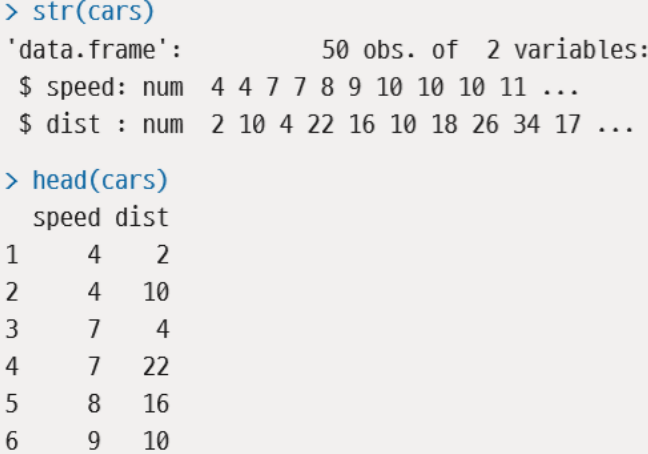
- plot()으로 가시화


- 설명 변수와 반응 변수 정하기
변수 사이 원인과 결과 따져 원인에 해당하는 것을 설명 변수로 함
- 단순 선형 회귀 : 설명 변수가 하나 뿐인 경우
모델 적합



- fitted 함수로 훈련 집합에 대한 예측 수행하기
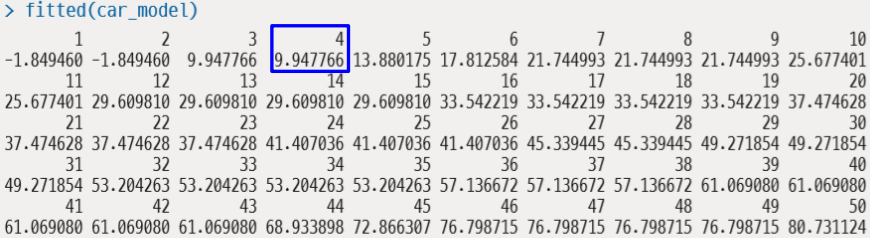
lm에 고차 방정식 적용
- lm은 기본적으로 1차 방정식, 즉 직선으로 모델 적합
- poly 옵션 사용하면 고차 방정식 적용 가능

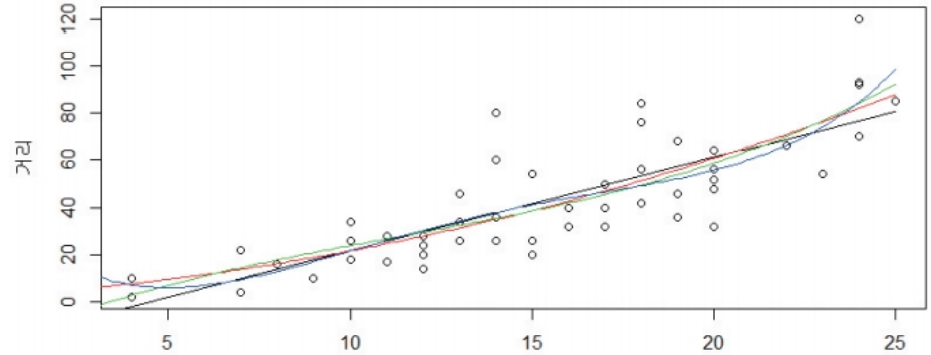
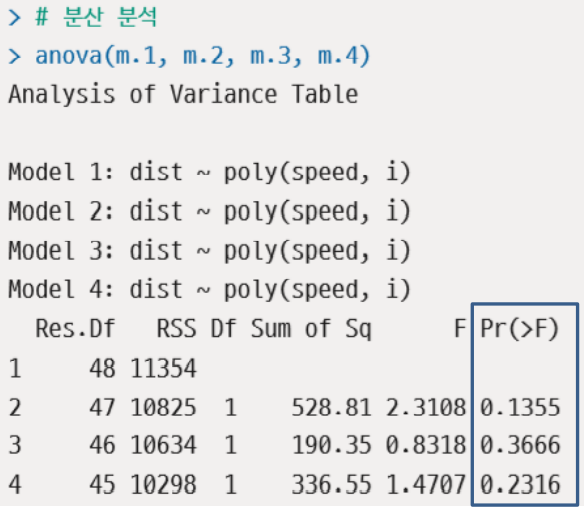
anova 함수로 분산 분석ANOVA(ANalysis Of VAriance) 해보기
- 여러 모델 간에 차이가 있는지에 대해 통계적 유의성 확인해 줌
현실 세계의 데이터는 설명 변수가 여러 개
- 월급에 영향을 미치는 변수로 판매 대수뿐 아니라 근무 연수, 직급 등
- 제동 거리에 영향을 미치는 변수로 속도뿐 아니라 날씨나 브레이크의 종류 등
다중 선형 회귀(multiple linear regression)
- 설명 변수가 2개 이상인 선형 회귀
- 설명 변수가 2개인 경우 매개변수 3개
- 일반적으로 설명 변수가 k개이면 매개변수는 k+1
'CS > R | DA' 카테고리의 다른 글
| R 일반화 선형 모델, 회귀, 분류, 결정트리, 랜덤 포레스트 (0) | 2021.06.10 |
|---|---|
| R 데이터 시각화, gapminder, 로그스케일, ggplot2 (0) | 2021.04.11 |
| R 데이터 가공, gapminder 라이브러리, 데이터 정렬 검색, 데이터 프레임 병합 (1) | 2021.04.10 |
| R 파일 입출력, 조건문, 반복문, 사용자 정의 함수, 결측값 처리, 이상값 (0) | 2021.04.08 |
| R read csv, R 데이터형, 벡터, 배열, 데이터프레임, 리스트 (0) | 2021.04.08 |




